Blog

Home

The Past, Present, and the Future of DNA Computing

I would be giving my Prelim (which essentially graduates me into a PhD candidate from a PhD student) in a couple of weeks and I am having serious questions about my intellect and my capability of finishing a PhD (and to be honest, surviving the prelim). But I somehow have to prepare some slides and pen a 30-page document, whilst I try to address the comments of a harsh reviewer who hated my first paper :3. Anyhow, I would be reading a lot of papers while preparing my slides. So I thought, why not compile them for the future, more intelligent MEs to peer at, and be less anxious! Maybe, this will motivate me to read the paper till the end. So, here goes.

Seesaw gates

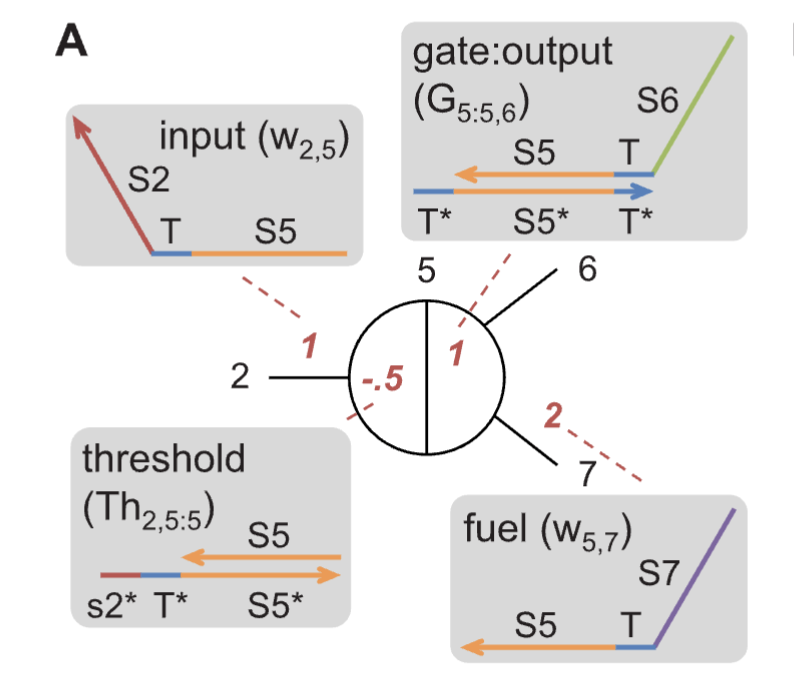
Qian and Winfree (2011) introduced the design of seesaw gates in the context of boolean logic computation. Each of these gates contain a base strand containing a “recognition” domain flanked on either sides by two toeholds. One of these toeholds is free, whereas the other is occupied by an incumbent signal strand. Seesaw gates enable catalytic signal transduction. The addition of the input displaces this outgoing strand, occupies the recognition domain, and opens up the previously bound toehold. A fuel strand then occupies this free toehold displacing the input back into its single-stranded form. Here, it is worth noting that each signal strand is designed such that it has a toehold in the middle, surrounding on the either side by recognition domains. Each of these recognition domains represent the gate they are returning from and the gate they are impinging upon, respectively.

Figure 1: Seesaw gate architecture

In the first stage, catalytic amplification and thresholding happens. A point to note is that these gates assume that the thresholding happens much faster than the strand displacement (increases the toehold length of $Th_{2,5:5}$ complex). The gate operation happens in two stages using two different seesaw gates. In the first stage, the output is generated and thresholded. In the second stage, the generated outputs from each of the upstream gates is integrated at the “Integration” gates. The final output is again thresholded and the rest is sent to the reporter for output generation.

By imposing the concentrations of the gates to be $1$ and the threshold to be around $0.6$, OR gate could be simulated and with a threshold of $1.2$, AND gate can be simulated. Note that at each gate, an output stoichiometrically equivalent to the gate complexes is produced.

Possible improvements

Reaction-Diffusion patterns in DSD-based CRNs

Dalchau, Seelig, and Phillips (2014) designed an extension for the VisualDSD framework to include spatial patterning by implementing PDE evaluators. They modeled the spatial patterns formed by various dynamical systems including, autocatalytic amplifier, Lotka-Volterra oscillator, and a consensus system. They simulated these systems both in the presence and absence of leaks.

In the autocatalytic amplifier, they observed travelling waves in the absence of leaks. However, they observed that this patter is highly sensitive to leak.

In the Lotka-Volterra oscillator, they observed periodic oscillatory waves, albeit with decreasing amplitude. Figure below shows these patterns.

Figure 2: Reaction-Diffusion patterns in a Lotka-Volterra oscillator.

More stable, equilibrium patterns were observed in the reaction-diffusion system of a majority consensus system. Remarkably, these patterns were qualitatively unaffected by leaks, as is the case with consensus algorithms.

Bibliography

Dalchau, Neil, Georg Seelig, and Andrew Phillips. 2014. “Computational Design of Reaction-Diffusion Patterns Using DNA-Based Chemical Reaction Networks.” In *DNA Computing and Molecular Programming*, 84–99. Springer International Publishing.
Garg, Sudhanshu, Shalin Shah, Hieu Bui, Tianqi Song, Reem Mokhtar, and John H Reif. 2018. “Renewable Time?responsive DNA Circuits.” *Small* 14: 1801470. <https://doi.org/10.1002/smll.201801470>.
Qian, Lulu, and Erik Winfree. 2011a. “Scaling up Digital Circuit Computation with DNA Strand Displacement Cascades.” *Science* 332 (6034): 1196–1201.
———. 2011b. “A Simple DNA Gate Motif for Synthesizing Large-Scale Circuits.” *J. R. Soc. Interface* 8 (62): 1281–97.
Reif, John H. 2011. “Scaling up DNA computation.” *Science* 332 (6034): 1156–57.
Seelig, Georg, David Soloveichik, David Yu Zhang, and Erik Winfree. 2006. “Enzyme-Free Nucleic Acid Logic Circuits.” *Science* 314 (5805): 1585–88.
Seelig, Georg, Bernard Yurke, and Erik Winfree. 2006. “Catalyzed Relaxation of a Metastable DNA Fuel.” *Journal of the American Chemical Society* 128 (37): 12211–20.
Garg, S. *et al.* (2019) ‘Nucleic acid hairpins: A robust and powerful motif for molecular devices’, in Zhang, Y. and Xu, B. (eds) *Invited chapter, from parallel to emergent computing*. World Scientific. doi:[10.1142/9789811201035_0007](https://doi.org/10.1142/9789811201035_0007).
Qian, L. and Winfree, E. (2011) ‘Scaling up digital circuit computation with DNA strand displacement cascades’, *Science*, 332(6034), pp. 1196–1201.
Reif, J.H. (2011) ‘Scaling up DNA computation’, *science*, 332(6034), pp. 1156–1157.
Seelig, G. *et al.* (2006) ‘Enzyme-free nucleic acid logic circuits’, *Science*, 314(5805), pp. 1585–1588.
Seelig, G., Yurke, B. and Winfree, E. (2006) ‘Catalyzed relaxation of a metastable DNA fuel’, *Journal of the American Chemical Society*, 128(37), pp. 12211–12220.