Blog
Home
Solving the 2024 IMO (well, atleast I’ll try)
Problem 1
Solution
\[m\alpha - 1 < \lfloor{m\alpha}\rfloor \leq m\alpha \ \ m\in \mathbb{Z}^+\\ \implies \dfrac{n(n+1)}{2} \alpha - n < \sum_{m=1}^n \lfloor{m\alpha}\rfloor \leq \dfrac{n(n+1)}{2} \alpha \\ \text{For the required sum to be a factor of } n, \ \ \exists k \in \mathbb{Z}^+ \ \ \sum_{m=1}^n \lfloor{m\alpha}\rfloor = kn \\ \dfrac{n(n+1)}{2} \alpha - n < kn \leq \dfrac{n(n+1)}{2}\alpha \\ \text{Cancelling } n \text{ as it is positive.} \\ \dfrac{(n+1)}{2} \alpha - 1 < k \leq \dfrac{(n+1)}{2}\alpha \\ \text{Given that $\alpha$ is a real number.} \\ -- \\ \mathrm{Case 1:} \dfrac{n+1}{2} \alpha > 0 \implies \alpha > 0 \\ -- \\ \mathrm{Case 2:} \dfrac{2k}{n+1} \leq \alpha < \dfrac{2(k+1)}{n+1} \ \ \ \forall k \in \mathbb{Z}^+ \\\]Problem 2
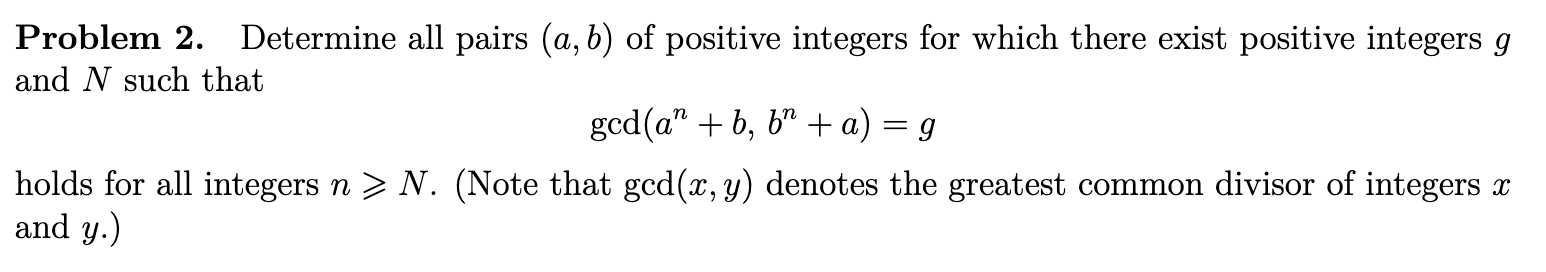
Solution
\[\text{There must exist some symmetry between } a \text{ and } b. \\ \text{This might require the application of the chinese remainder theorem.}\]